Contents
- init
- first 2 branches, run arclength from the start
- branch 3: use tomsol for initial steps, then switch to arclength
- plot BD, amplitude, L^2
- plot BD, T
- plot solns
- check swiparf, e.g, switch to continuation in c_5
- plot BD
- plot solns
- stability checks
- time-integration (repeat if necessary)
- x-t plot: see in ts if there's something interesting after np periods,
clear all;close all;format compact;clear classes;
init
ndim=1; dir='hom1d'; p=[]; lx=pi; nx=30; % domain size and spat.resolution par=[-0.05; 1; 0.1; -1; 1]; % r nu mu c3 c5 p=cGLinit(p,lx,nx,par,ndim); p=setfn(p,dir); p.sol.ds=0.1; p.nc.dsmax=0.2; p.sw.bifcheck=2; p.nc.neig=10; p=cont(p,20);
first res=0 Problem directory name: hom1d step lambda y-axis residual iter meth ds #-EV 0 got first point with lam=-0.05, res=0 - now lam=-0.04 1 got second point with lam=-0.04, res=0 - 1 possible bif between -0.04 and 0.060381, om=0 mu_r=-9.35645e-05, mu_i=-1 2 9.35645e-05 (HP, saved to hom1d/hpt1.mat) bisection steps 10, last ds -4.88281e-05 3 0.06038 0.000e+00 0.00e+00 0 nat 0.10000 2 4 0.16076 0.000e+00 0.00e+00 0 nat 0.10000 2 - 1 possible bif between 0.160762 and 0.261143, om=0 mu_r=-6.08607e-05, mu_i=-1 5 2.50262e-01 (HP, saved to hom1d/hpt2.mat) bisection steps 10, last ds -4.88281e-05 6 0.26114 0.000e+00 0.00e+00 0 nat 0.10000 4 7 0.36152 0.000e+00 0.00e+00 0 nat 0.10000 4 8 0.46190 0.000e+00 0.00e+00 0 nat 0.10000 4 9 0.50000 0.000e+00 0.00e+00 0 nat -0.06205 4 10 0.56229 0.000e+00 0.00e+00 0 nat 0.10000 4 11 0.66267 0.000e+00 0.00e+00 0 nat 0.10000 4 ...
first 2 branches, run arclength from the start
para=4; ds=0.1; figure(2); clf; for bnr=1:2 switch bnr case 1; p=hoswibra('hom1d','hpt1',ds,para,'1db1'); nsteps=25; case 2; p=hoswibra('hom1d','hpt2',ds,para,'1db2'); nsteps=20; end p.hopf.jac=1; p.nc.dsmax=0.5; p.hopf.xi=0.05; p.fuha.blss=@mbel; p.nc.mbw=2; p.hopf.ilss=0; % set to 0 if no ilupack t1=tic; p=cont(p,nsteps); toc(t1) end
Problem directory name: 1db1 real(mu)=-9.35645e-05, imag(mu)=1 lam=9.35645e-05, om=1, NF-coeffis: dlam=-1, alpha=4.06202 arc.parametr, lambda-guess=4.1236e-06 max|y-u0|=0.604114, res=0.000463596 step lambda y-axis res iter ds T nT 1 6.776e-21 0.00323 3.63e-09 2 -0.01900 6.34e+00 2 -0.00004 0.00645 1.077e-13 3 0.20000 6.33540 21 0.00139 -0.00219 3 -0.00163 0.04043 6.198e-09 1 0.40000 6.33641 21 0.00870 -0.01369 poor solve in mbel, |r|=0.00262868, b(end)=1, iterating ...it=1, |r|=2.14786e-07 4 -0.01161 0.10837 1.520e-14 2 0.40000 6.34283 21 0.02337 -0.03594 poor solve in mbel, |r|=0.00776395, b(end)=1, iterating ...it=1, |r|=8.98535e-08 5 -0.03011 0.17628 6.037e-14 2 0.40000 6.35513 21 0.03814 -0.05611 poor solve in mbel, |r|=0.0298035, b(end)=1, iterating ...it=1, |r|=1.72901e-05 6 -0.05605 0.24413 8.285e-14 2 0.40000 6.37336 21 0.05308 -0.07292 poor solve in mbel, |r|=0.151921, b(end)=1, iterating ...it=1, |r|=6.34526e-05 ...
branch 3: use tomsol for initial steps, then switch to arclength
ds=0.2; p=hoswibra('hom1d','hpt3',ds,3,'1db3'); p.hopf.xi=0.05; p.hopf.jac=1; p.nc.dsmax=0.5; p.hopf.tom.AbsTol=1e-5; p.hopf.tom.RelTol=5e-4; p=cont(p,5); p.sw.para=4; p=cont(p,10);
Problem directory name: 1db3
real(mu)=9.79984e-05, imag(mu)=1
lam=1.00312, om=1, NF-coeffis: dlam=-1, alpha=3.13786
nat.parametr, lambda-guess=0.803119
step lambda y-axis res iter ds T nT
===> Non linear iteration = 1, Linear iteration = 1
N= 20, Maximum relative error = 2.02884, order = 2
===> Non linear iteration = 2, Linear iteration = 1
N= 20, Maximum relative error = 4.58471, order = 2
===> Non linear iteration = 3, Linear iteration = 1
N= 20, Maximum relative error = 0.0714659, order = 2
===> Non linear iteration = 4, Linear iteration = 1
N= 20, Maximum relative error = 0.0145202, order = 2
===> Non linear iteration = 4, Linear iteration = 2
N= 40, Maximum relative error = 0.0142335, order = 2
===> Non linear iteration = 5, Linear iteration = 1
N= 40, Maximum relative error = 0.00197695, order = 2
#### The solution was obtained on a mesh of 41 points
The maximum relative error is 0.00197695
There were 228 calls to the ODE function.
...
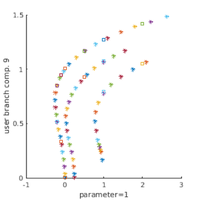
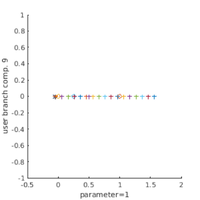
plot BD, amplitude, L^2
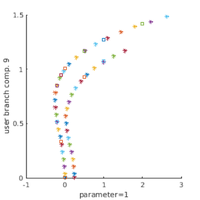
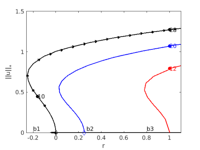
bpcmp=9; wnr=3; figure(wnr); clf plotbraf('hom1d','pt21',3,bpcmp,'ms',0); plotbraf('1db1','pt34',3,bpcmp,'lab',[10, 28]); plotbraf('1db2','pt22',3,bpcmp, 'lab', 20,'cl','b'); plotbraf('1db3','pt17',3,bpcmp, 'lab', 12,'cl','r','ms',0); axis([-0.26 1.1 0 1.5]); xlabel('r'); ylabel('||u||_*'); text(-0.2,0.05,'b1','fontsize',16);text(0.27,0.05,'b2','fontsize',16); text(0.8,0.05,'b3','fontsize',16); p=loadp('hom1d','hpt1'); k2=0; rstep=0.1; plotana1(k2,rstep,'k*',1);
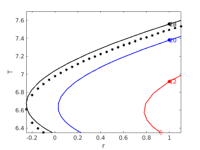
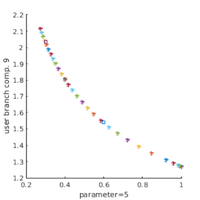
plot BD, T
bpcmp=6; wnr=3; figure(wnr); clf plotbraf('1db1','pt34',3,bpcmp, 'lab',28, 'fp',1); plotbraf('1db2','pt22',3,bpcmp, 'lab', 20,'cl','b','fp',1); plotbraf('1db3','pt17',3,bpcmp, 'lab', 12,'cl','r','fp',1); axis([-0.25 1.1 6.35 7.7]); xlabel('r'); ylabel('T'); % add comparison to analytical soln p=loadp('hom1d','hpt1'); k2=0; rstep=0.05; plotana1(k2,rstep,'k*',2);
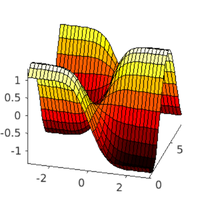
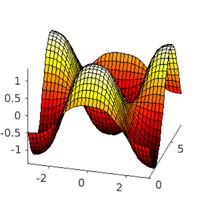
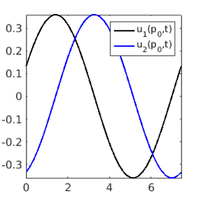
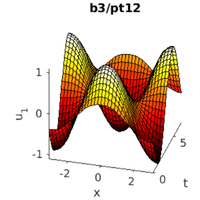
plot solns
hoplotf('1db1','pt10',1,1); figure(1); title('b2/pt10'); xlabel('x'); ylabel('t'); zlabel('u_1'); pause; hoplotf('1db2','pt20',1,1); figure(1); title('b2/pt20'); xlabel('x'); ylabel('t'); zlabel('u_1'); pause; hoplotf('1db3','pt12',1,1); figure(1); title('b3/pt12'); xlabel('x'); ylabel('t'); zlabel('u_1');
lam=-0.160067 lam=1 lam=1
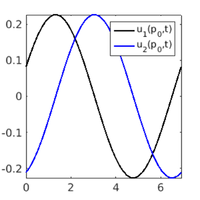
check swiparf, e.g, switch to continuation in c_5
p=swiparf('1db1','pt28','c5b',5); clf(2); getaux(p) p.sol.restart=1; p.sol.ds=-0.05; p.nc.dsmax=0.2; p.sw.para=3; p=arc2tom(p); p.usrlam=[0.25 0.3 0.4 0.6]; p.hopf.xi=0.01; p=hoinistep(p,ds); p.sw.para=4; p.hopf.tau=[]; p=cont(p,30);
Problem directory name: c5b
Problem directory name: c5b
ans =
1.0000
1.0000
0.1000
-1.0000
1.0000
===> Non linear iteration = 1, Linear iteration = 1
N= 20, Maximum relative error = 0.00823065, order = 2
#### The solution was obtained on a mesh of 21 points
The maximum relative error is 0.00823065
There were 42 calls to the ODE function.
There were 2 calls to the BC function.
hoinistep got 1st point
1 0.99188 1.27581 1.659e-10 2 -0.01000 7.56657 21 0.000e+00 0.000e+00
===> Non linear iteration = 1, Linear iteration = 1
N= 20, Maximum relative error = 0.00829278, order = 2
#### The solution was obtained on a mesh of 21 points
The maximum relative error is 0.00829278
...
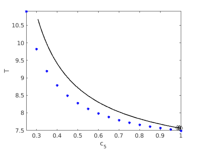
plot BD
bpcmp=6; pstyle=3; wnr=3; figure(wnr); clf plotbraf('c5b','pt30',3,bpcmp); xlabel('c_5'); ylabel('T'); p=loadp('c5b','pt35'); plotana2(p,0,5,0.25,1,0.05,'b*',2,1); axis tight;
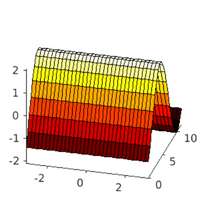
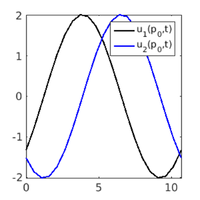
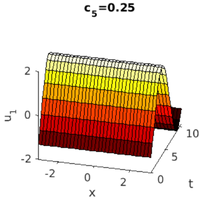
plot solns
hoplotf('1db1','pt28',1,1); figure(1); title('c_5=1'); xlabel('x'); ylabel('t'); zlabel('u_1'); pause; hoplotf('c5b','pt30',1,1); figure(1); title('c_5=0.25'); xlabel('x'); ylabel('t'); zlabel('u_1');
lam=1 lam=0.306384
stability checks
scsw=3; % choose switch scsw case 1; p=loadp('1db1','pt10'); hoplot(p,1,1); dir='stab1d1'; case 2;p=loadp('1db1','pt28'); hoplot(p,1,1); dir='stab1d2'; case 3; p=loadp('1db2','pt20'); hoplot(p,1,1); dir='stab1d3'; end p.u(1:p.nu)=p.hopf.y(1:p.nu,1); u0=p.u(1:p.nu); p=setfn(p,dir); ts=[]; t0=0; npp=50; nt=200; pmod=50; smod=5; tsmod=1; nc=0;
Problem directory name: stab1d3
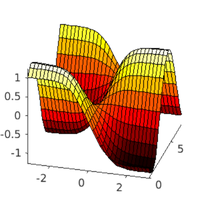
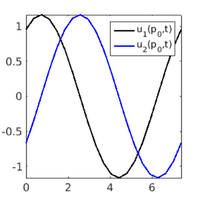
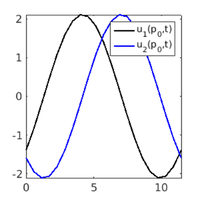
time-integration (repeat if necessary)
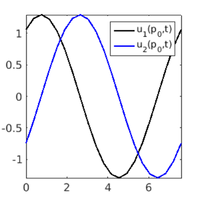
nt=400; [p,t0,ts,nc]=hotintxs(p,u0,t0,ts,npp,nt,nc,tsmod,pmod,smod,@nodalf,1); figure(4); clf; plot(ts(1,:), ts(2,:)); % plot values at selected point figure(5); clf; plot(ts(1,:), ts(3,:)); % plot difference in norm set(gca,'FontSize',p.plot.fs); axis tight; xlabel('t'); ylabel('||u(t)-u_0||_{\infty}');
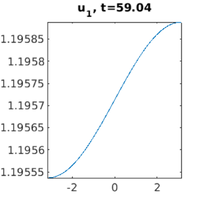
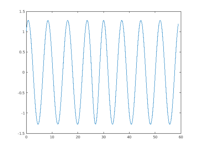
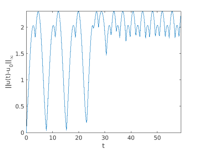
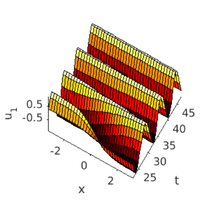
x-t plot: see in ts if there's something interesting after np periods,
then plot around there
si=3*npp, incr=5; nt=5*npp/smod, wnr=2; cmp=1; vv=[30,70]; nt=35; tintplot1d(dir,si,incr,nt,wnr,cmp,vv); xlabel('x'); ylabel('t'); zlabel('u_1'); set(gca,'ZTick',[-0.5 0.5]);
si =
150
nt =
50