Contents

% driver script for Shallow Lake Optimal Control
path('../tom',path); path('../p2poclib',path); format short; format compact;
close all; clear all; global s0 s1 u0 u1 Psi par xi um1 um2 sig;

Preparations: put filenames into fn, set some bvp parameters

sd0='f1'; sp0='pt12'; sd1='p3'; sp1='pt11'; flip=1; % p3->FSC
fn=setfnflip(sd0,sp0,sd1,sp1,flip); opt=[]; opt=ocstanopt(opt);
opt.rhoi=1; opt.t1=100; opt.start=1; opt.tv=[]; opt.nti=10; opt.retsw=0;

the solve and continue call, and some plots

sol=[]; alvin=[0.1 0.25]; v=[15,30]; opt.msw=1;
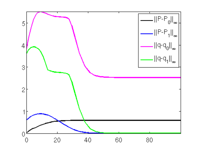
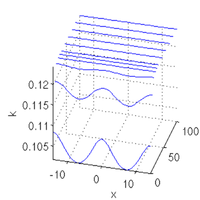
[alv,vv,sol,udat,tlv,tv,uv]=iscnat(alvin,sol,[],opt,fn); slsolplot(sol,v);

ans =
    0.0300    0.6500    0.5000    0.5000
ans =
    0.0300    0.6500    0.5000    0.5000
getting Psi, done in 0.045225 sn/2=102, d=0, suggested T=39.5764
al=0.1, flag=0 
al=0.25, flag=0
   
a subsequent call to iscnat
opt.tv=sol.x; opt.start=0; alvin=[0.25 0.5 0.7 1];  opt.msw=1; opt.vsw=0;
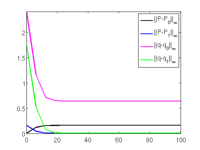
[alv1,vv1,sol,udat,tlv1,tv1,uv1]=iscnat(alvin,sol,udat.usec,opt,fn);
alv=[alv alv1]; vv=[vv vv1]; tlv=[tlv tlv1]; tv=[tv; tv1]; uv=[uv; uv1];

secant pred., al=0.25
al=0.25, flag=0
secant pred., al=0.5
al=0.5, flag=0
secant pred., al=0.7
al=0.7, flag=0
secant pred., al=1
al=1, flag=0

---- A fold in alpha, here iscarc needed. Prep. and initial iscarc call
sd0='f1'; sp0='pt12'; sd1='p1'; sp1='pt71'; flip=1; fn=setfnflip(sd0,sp0,sd1,sp1,flip);
esol=[]; usec=[]; opt.nsteps=3; opt.alvin=[0.2 0.25]; sig=0.1; opt.nti=10; opt.tv=[];
opt.Stats_step='on'; opt.start=1; opt.sigmax=1; opt.retsw=1;
[alv,vv,usec1,esol1,tlv,tv,uv]=iscarc(esol,usec,opt,fn); opt.start=0;

iscarc, calling iscnat
ans =
    0.0300    0.6500    0.5000    0.5000
ans =
    0.0300    0.6500    0.5000    0.5000
getting Psi, done in 0.044723 sn/2=102, d=0, suggested T=39.5764
===> Non linear iteration  = 1, Linear iteration = 1 
     N= 10, Maximum relative error = 11.5008, order = 2 
===> Non linear iteration  = 2, Linear iteration = 1 
     N= 10, Maximum relative error = 0.120916, order = 2 
...
  
subsequent iccarc-calls (repeat this cell)
opt.nsteps=35; usec=usec1; esol=esol1; % new input (for repeated calls)
[alv1,vv1,usec1,esol1,tlv1,tv1,uv1]=iscarc(esol,usec,opt,fn);
% append output to prev. steps for repeated calls
alv=[alv alv1]; vv=[vv vv1]; tlv=[tlv tlv1]; tv=[tv; tv1]; uv=[uv; uv1];

i=1, sig=0.033275
 ===> Non linear iteration  = 1, Linear iteration = 1 
     N= 40, Maximum relative error = 0.00190948, order = 2 
flag=0, al=0.346832, delta-al=0.016169
i=2, sig=0.0366025
 ===> Non linear iteration  = 1, Linear iteration = 1 
     N= 40, Maximum relative error = 0.00347219, order = 2 
flag=0, al=0.361696, delta-al=0.0148643
i=3, sig=0.0402628
 ===> Non linear iteration  = 1, Linear iteration = 1 
...
save results for skibademo.m
alv0=alv; vv0=vv; tv0=tv; uv0=uv; tlv0=tlv;

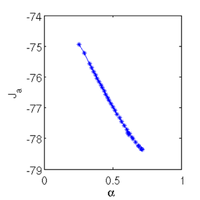
a simple plot of J over alpha
figure(6); clf; plot(alv(1,:),vv(1,:),'-*'); set(gca,'FontSize',s1.plot.fs);
xlabel('\alpha','FontSize',s1.plot.fs); ylabel('J_{a}','FontSize',s1.plot.fs);

 
save a path
usec=usec1; sols=esol1; % only update (for saving) after success in iccarc!
save('p71toFSC','fn','Psi','xi','alv','vv','tlv','sols','tv','uv','usec','sig','um1','um2','opt');

load again (typically for later plotting)
[fn,alv,vv,tlv,esol1,tv,uv,usec1,opt]=loadcp('p71toFSC');

evaluate selected path from continuation
j=length(tlv); %j=22; j=34; j=5;
tl=tlv(j); v=[25,15]; n=s1.nu; sol.x=tv(j,1:tlv(j));sol.y=squeeze(uv(j,1:n,1:tlv(j)));
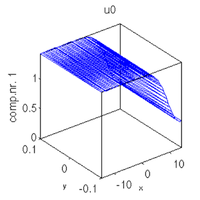
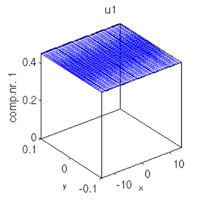
al=alv(j), u0=al*s0.u(1:n)+(1-al)*s1.u(1:n); u1=s1.u(1:s1.nu); slsolplot(sol,v);

al =
    0.6070

   
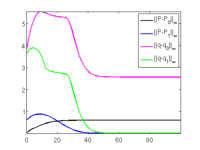
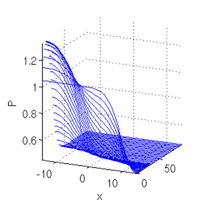
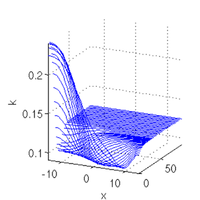
values;
rho=s1.u(s1.nu+1); jp=jcai(s1,sol,rho)+disjca(s1,sol,rho); % jca of path
j0=jca(s0,s0.u)/rho; j1=jca(s1,s1.u)/rho; al=alv(end); % jcas of CSS
fprintf([fn.sd0 '/' fn.sp0 ' to ' fn.sd1 '/' fn.sp1 ', al=' mat2str(al,3) ': ']);
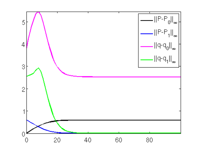
fprintf('J0=%g, Jp=%g, J1=%g\n',j0,jp,j1); zdia=sldiagn(sol,15);
tit=['J_0=' mat2str(j0,5) ',  J=' mat2str(real(jp),5) ',  J_1=' mat2str(j1,5)]; title(tit);

p1/pt71 to f1/pt12, al=0.607: J0=-78.9265, Jp=-77.824, J1=-72.9539

 
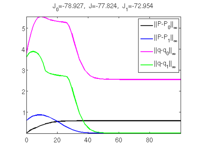
fix al from iscarc to some given value and compute CPs
j=22; n=s1.nu; sol.x=tv(j,1:tlv(j));sol.y=squeeze(uv(j,1:n,1:tlv(j)));
al=0.6; u0=al*s0.u(1:n)+(1-al)*s1.u(1:n); u1=s1.u(1:s1.nu);
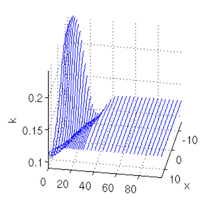
opt.M=s1.mat.M; sol=mtom(@mrhs,@cbcf,sol,opt); v=[100,30]; slsolplot(sol,v);

===> Non linear iteration  = 1, Linear iteration = 1 
     N= 40, Maximum relative error = 0.00266071, order = 2 

   
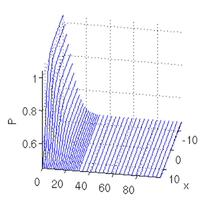
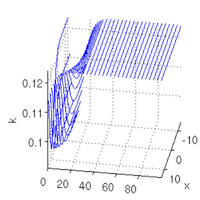
now the same on lower branch
j=34; n=s1.nu; sol.x=tv(j,1:tlv(j));sol.y=squeeze(uv(j,1:n,1:tlv(j)));
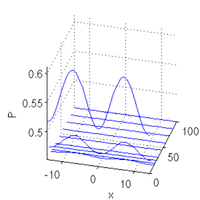
al=0.6; sol=mtom(@mrhs,@cbcf,sol,opt);  slsolplot(sol,v);

===> Non linear iteration  = 1, Linear iteration = 1 
     N= 40, Maximum relative error = 0.00879275, order = 2 

   


      Published with MATLAB® 7.14