

Anschaulicher Forschungsüberblick der AG Angewandte Analysis und Mathematische Modellierung
Differentialgleichungen, insbesondere
partielle Differentialgleichungen, spielen eine fundamentale Rolle in der
Beschreibung oder Modellierung
von Naturvorgängen. Nahezu die gesamte Theoretische Physik ist in
Form von Differentialgleichungen formuliert. In diesem Zusammenhang
meint Analysis die Untersuchung der Gleichungen auf klassische
Weise, d.h. durch Nachdenken mit Papier und Bleistift und im wesentlichen
ohne Computer.
Dabei werden oft die Gleichungen nicht eigentlich gelöst, sondern
nur Eigenschaften der Lösungen beschrieben.
Neben der Analysis spielt jedoch auf Grund immer höherer Computerleistungen die
sogenannte numerische Lösung oder Simulation der partiellen Differentialgleichungen eine wichtige Rolle;
Numerik
erlaubt, Phänomene quantitativ
zu berechnen, die durch Experimente kaum zu studieren sind. Das Naturverständnis kann verbessert
werden, kostspielige Versuchsanordnungen können entfallen, wertvolle Rohstoffe können eingespart werden. Die mathematische Vorausberechnung technischer Prozesse hat eine immense Bedeutung für zahlreiche Schlüsselbereiche der Wirtschaft.
Trotz immer schnellerer Rechner wird es aber auch in Zukunft im allgemeinen unmöglich bleiben, räumlich dreidimensionale Probleme oder Probleme mit
komplexer
Dynamik ohne dem Problem angepasste Verfahren numerisch befriedigend zu lösen, d.h. ein numerisches Lösen von Differentialgleichungen setzt zuerst ein analytisches Verständnis dieser voraus. Hier folgen zwei Beispiele für Arbeitsgebiete der AG, in denen Analysis zunächst
zur Klärung grundlegender Fragen beiträgt, und dann zum Teil im Wechselspiel
mit Numerik auch quantitative Berechnungen ermöglicht. Für Details (z.B. die Gleichungen!)
verweisen wir auf die Publikationen, siehe
Forschung
(oder english version).
Modelle der Nichtlinearen Optik
Die digitale Datenübertragung in einem
Glasfaserkabel geschieht grob vereinfacht dadurch, dass
Nullen und Einsen nacheinander übertragen werden.
Die physikalische Realisierung einer 1 geschieht durch
einen kurzen Lichtpuls.
Dieser besteht physikalisch gesehen aus einer modulierten
elektromagnetischen Welle.
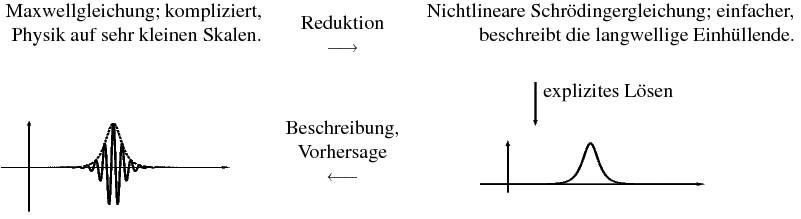
Die numerische Simulation
dieses System in einem 1000km langen Kabel mittels
der Maxwellgleichungen ist unmöglich:
Die Wellenlänge von Licht ist im Mikrometer Bereich,
d.h. ca. 10^(-6)m.
Um die elektromagnetische Welle aufzulösen, muss
das Kabel also in ca 10^(-9)m lange Teile zerlegt werden.
Bei einer Länge von 1000km= 10^6m ergeben sich also
insgesamt 10^12 Punkte, zuzüglich radialer Richtungen des Kabels
und Zeitdiskretisierung, eine selbst für moderne Computer
viel zu große Zahl. In nichtlinearen Medien wie Glasfasern wird daher
üblicherweise eine Näherungsgleichung,
die (nichtlineare)
Schrödingergleichung,
für die Einhüllende des Pulses hergeleitet, was zu einer gewaltigen
Dimensionsreduktion führt.
In vielen Fällen lässt sich mathematisch zeigen,
dass diese Näherung richtige Vorhersagen erlaubt.
 |
Ein relativ neues Forschungsgebiet in diesem Zusammenhang ist die (mathematische)
Plasmonik ,
bei der die Interaktion von Licht und
Metallen untersucht wird; hier arbeiten wir u.a. mit
dem IfP
zusammen.
Musterbildung und Selbstorganisation
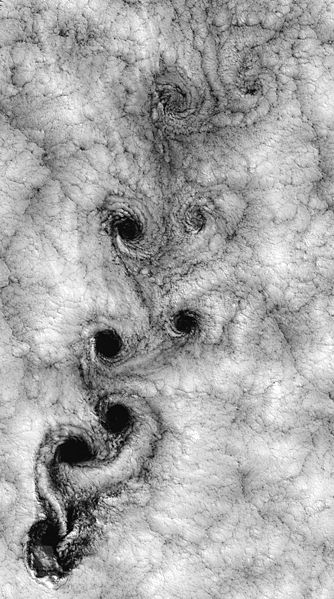
Komplexe Strukturen (z.B. Muster in Tierfellen, in Wolken, in Sand,
in Strömungen) in der Natur werden häufig durch sogenannte
Selbstorganisation erzeugt, auf diversen Skalen, z.B.
(klicke auf Bilder für weitere Infos, alle aus
wikipedia commons):
Spiralgalaxie
NGC 6384, Great Red Spot of Jupiter


Wirbelstrasse hinter Juan Fernandez Inseln,
"Tiger-Bush" Vegetationsmuster, "Roll Cloud"


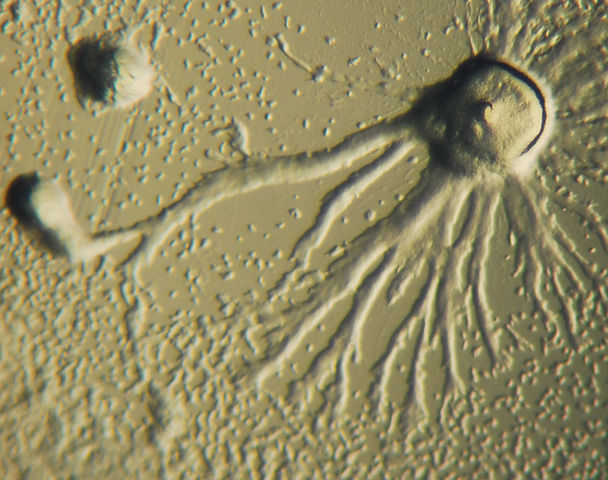
Dünen im Erg Chebbi Jaguar, Kastenfisch,



Orchidee, Tintenfisch, Dictyostelium (Bakterium)


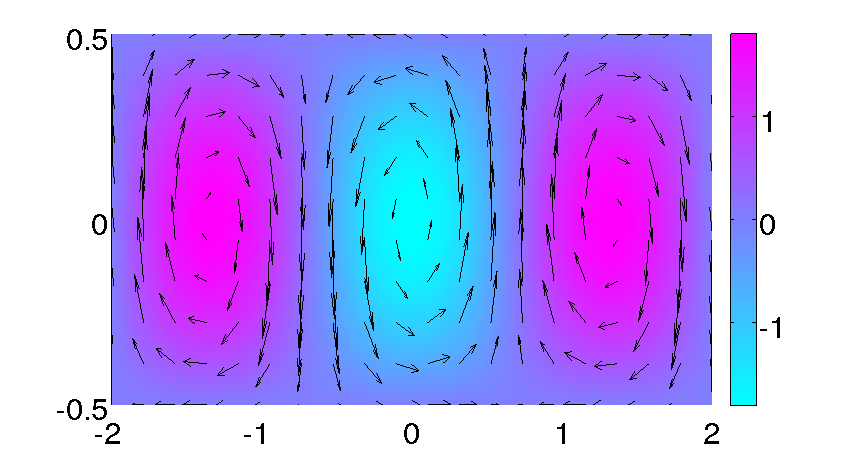
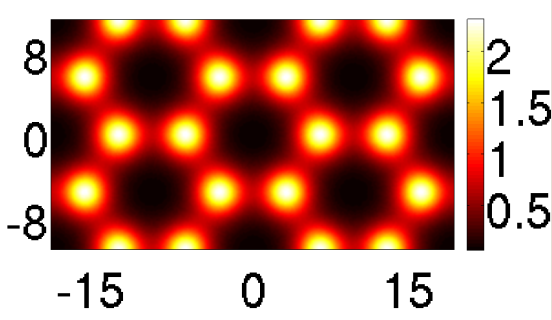
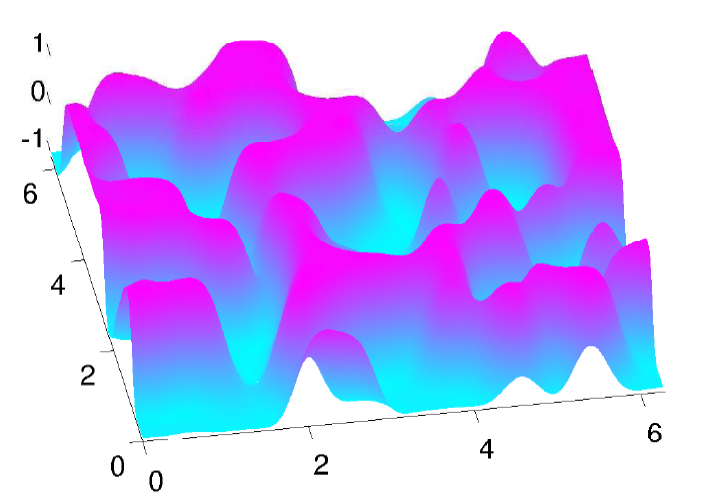
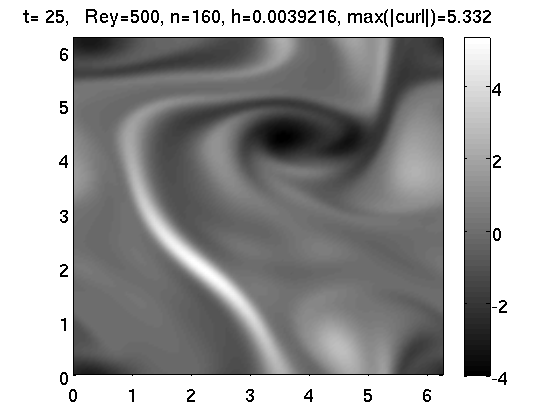
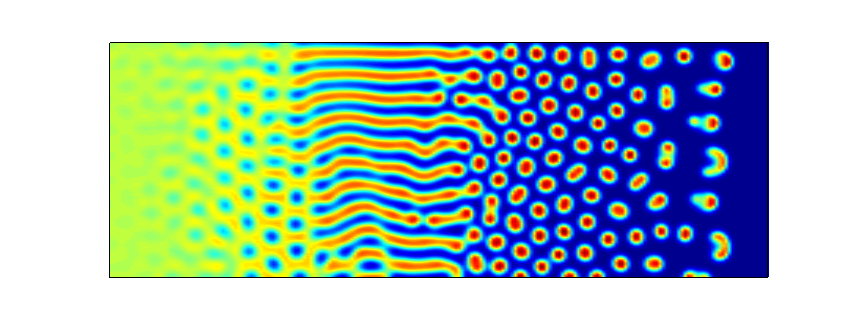
Hier einige (einfache) eigene Simulationen zu:
Konvektionsrollen im Rayleigh-Benard system,
ein Muster im Schnakenbergsystem, Phasentrennung in der 2D Allen-Cahn Gleichung,
eine 2D Navier--Stokes Simulation, und Bakterienmuster im Watt
 >
>
|
Es gibt eine Reihe von physikalischen Experimenten (z.B. das
Benardproblem), oder das
Taylor-Couette-Problem,
anhand derer diese Vorgänge untersucht werden.
Auch hier sind die zugehörigen Modelle
partielle Differentialgleichungen, z.B. in der Form von
Reaktions-Diffusionssystemen
oder der
Navier--Stokes Gleichungen.
Obwohl vollkommen verschiedene physikalische oder biologische Systeme betrachtet werden,
weisen sie alle das gleiche universelle Verhalten auf.
Grundlegende Vorhersagen zu Mustern (Wellenlänge, prinzipielle Form,
Parameterbereich des ersten Auftretens, erste Stabilitätsanalysen)
sollten und können dabei wieder analytisch gewonnen werden, denn
der Instabilitätsmechanismus der trivialen Lösung ist oft die
Turing--Bifurkation.
Ähnlich wie bei der Reduktion von Wellengleichungen zur Nichtlinearen
Schrödingergleichung führt hier ein Skalenseparierung zu vereinfachten
Gleichungen vom Ginzburg--Landau Typ.
Zur Verfolgung verzweigender Lösungen nach der Bifurkation und zum Aufspüren weiterer
Bifurkationen wird Analysis meist mit Numerik in
numerischer Pfadverfolgung
kombiniert. Hierzu haben wir kürzlich das Paket
PDE2path
für 2D elliptische Systeme entwickelt.
In Zusammenarbeit mit dem ICBM
untersuchen wir gegenwärtig Systeme zur
Beschreibung der Musterbildung von Bakterien im Watt.
Ausserdem: Quorum sensing ...
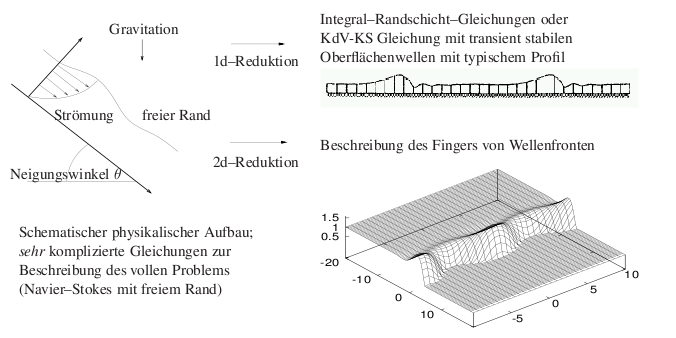
Instabilitäten von Filmströmungen
Die Strömung eines Flüssigkeitsfilmes ist ein physikalisches
System mit unzähligen technischen Anwendungen wie z.B. der
Beschichtung einer Folie oder schlicht dem Wischen einer Tafel
oder einer Windschutzscheibe. Das System besitzt eine ausgesprochen
interessante Dynamik, welche mathematisch
bislang nicht gut verstanden ist. Wieder erhält man hier durch
Reduktionsmethoden wichtige Einblicke.
 |
Ausblick
Dieser kurze Überblick sollte beispielhaft einige Forschungsprojekte
andeuten und vermitteln, dass die Angewandte Analysis sich aus
mathematischer Sicht mit aktuellen naturwissenschaftlichen
und technischen Fragestellungen beschäftigt. Der besondere Reiz besteht
dabei stets in Wechselspiel und gegenseitiger Befruchtung zwischen Mathematik und
Anwendungen, welche immer wieder zu neuen Forschungen Anlass geben: neue Fragestellungen verlangen oft eine neue Mathematik,
und andererseits erlaubt die Anwendung von in anderem Zusammenhang
gewonnenen neuen mathematischen Methoden die Lösung
(oder effizientere Lösung) von Anwendungsproblemen.
Weitere Informationen inkl. Veröffentlichungen zur Forschung der Arbeitsgruppe Angewandte Analysis und Mathematische Modellierung finden
Sie z.B. hier.













 >
>




