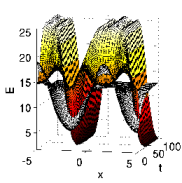
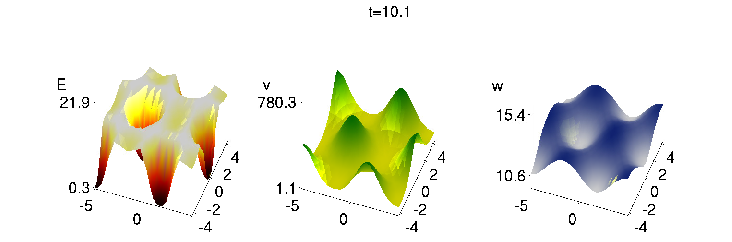
p2pOC: a pde2path add-on library for solving spatially distributed optimal control problems.

p2poc: a pde2path add-on library for solving infinite time horizon spatially distributed optimal control problems.

Current version (0.2) written and maintained by H. Uecker

p2poc is now (April 2016) contained in pde2path v2.2, including the OC demos sloc and vegoc. The basic setup in the OC Quickstart Guide still applies, but the download of p2poc.tar.gz below rather applies to pde2path 2.0.

p2poc is an add-on toolbox to the Matlab package pde2path (v2.0). It aims at the numerical solution of infinite time horizon optimal control (OC) problems for parabolic systems of PDE over 1D or 2D spatial domains. The basic idea is to treat the OC problem via the associated canonical system in two steps. First we use pde2path to find branches of stationary solutions of the canonical system, also called canonical steady states (CSS). In a second step we use the results and the spatial discretization of the first step to calculate the objective values of time-dependent canonical paths ending at a CSS with the so called saddle point property. This is a (typically very high dimensional) boundary value problem (BVP) in time, which we solve by combining a modification of the BVP solver TOM with a continuation algorithm in the initial states.

Initially, the software was written with the help of Dieter Grass for the Shallow Lake OC (SLOC) problem studied in [GU15] , and implements some ideas of Dieter used in OCMat . See also his paper [G15] on (1D) spatially distributed OC problem using finite differences and OCMat. Thanks to Dieter for clarifying (and posing) many questions regarding the aim of software based on Pontryagin's Maximum Principle for spatially distributed OC problems. The error's in p2poc are all mine.

p2poc is also used in [U15] for a vegetation OC problem (vegOC), and a number of further applications are underway.

Our modification MTOM of TOM is only ad-hoc, and in this sense p2poc currently has beta-status. MTOM works, but it will be replaced by an official version of TOM which handles mass matrices "M" once that becomes available.

Download: Quickstart Guide, and p2poc.tar.gz (software and demos); this contains p2plib which is originally a part of pde2path. For background you might also want to get p2p2.tar.gz (which contains the pde2path DEMOS), and the Original Manual and V2.0 Manual

New: version 0.2 now contains an interface to OOPDE, which can be used to run p2poc (and pde2path) in a genuine 1D setup (in a very rudimentary way), which gives a significant speedup compared to the old quasi-1D setup of thin strips.

Thus, the p2plib that comes with p2poc is an extension of the p2plib which comes with pde2path2.0. However, pde2path2.0 files should still run with this new p2plib.
The old p2poc version 0.1 can be found here.
pde2path itself will also be upgraded to OOPDE when more features of OOPDE will be linked into p2plib, including 3D problems. For now we include a version OOPDElight, which provides basic features of OOPDE. User with matlab versions older than 2013a can use OOPDElightNA (No Abstract class attributes) instead of OOPDElight.

To get started

unpack p2poc.tar.gz
create a subdirectory tom of p2poc, get TOM from here and put the files tominit.m, tomget.m and tomset.m into the subdirectory tom
(of course we also recommend to get and use tom.m as a general BVP solver)
change into one of the demo directories slocdemo or vegdemo. In slocdemo execute the script-files bdcmds.m, cpdemo.m and skibademo.m, usually "cell-by-cell" to see what's happening. Similarly, in vegdemo execute bd1ddemo.m, vegcpdemo.m, and skiba.m. To explore the interfaces to OOPDE including the genuine 1D setting explore the oosloc or oovegoc directories.

Step 3 assumes the directory structure from steps 1,2; alternatively, adapt the first cells of the script files to set the matlab path as needed.
The demo directories contain more script files, for instance some basic 2D simulations.
Have a look at the Quickstart Guide, and the m-files in p2poclib for more information.

The demo-files contain the basic setup and scripts used for [GU15] and [U15] . Verbatim outputs of these demo-files and some more results are here:

SLOC: bdcmds_pub (CSS bifurcation diagram), cpdemo_pub (Canonical paths demo), skibademo_pub (Calculation of a Skiba point, aka indifference point)
vegOC: bd1ddemo (1D bifurcation diagram), cpdemo (canonical paths), and skiba
Canonical path movies for 2D SLOC and 2D vegOC: The control path to go from a PCSS to the FSC (SLOC, left), and to go from the FSC to a hexagonal harvesting strategy (vegOC, right).

To start your own simulations, copy files from, e.g., slocdemo in case of a scalar state PDE, into a new directory to files *init.m, *sG.m, and so on, with * the name of your model, and start modifying these files. In case you have a system of PDEs for the states we recommend to copy and modify the files from vegdemo.

For bugs, questions or remarks please write to: hannes.uecker -- at -- uni-oldenburg.de. Any feedback is welcome.

References

[G15] D. Grass From 0D to 1D spatial models using OCMat , Technical Report, ORCOS, 2015.
[GU15] D. Grass, H. Uecker Optimal management and spatial patterns in a distributed shallow lake model, Preprint, 2015.
[U15] H. Uecker, Optimal control and spatial patterns in a semi arid vegetation system Natural resource modeling, 2016, Preprint, 2015