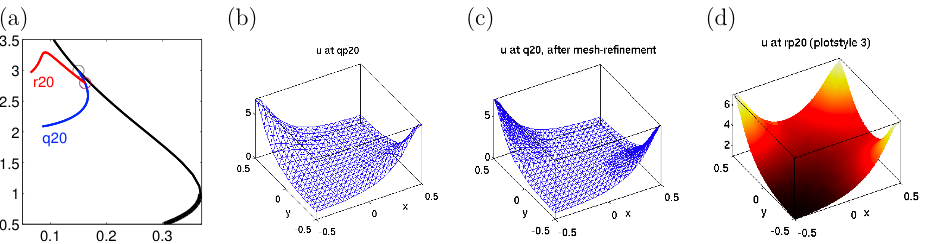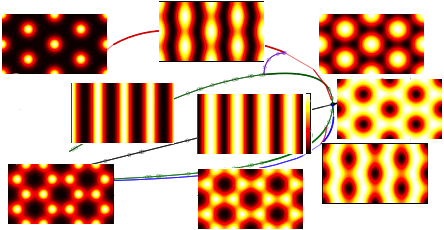
$\def\R{\mathbb R}\def\lam{\lambda}\def\Om{\Omega}\def\pa{\partial}$ $\def\huga#1{\begin{gather} #1 \end{gather}}$ $\newcommand{\spr}[1]{\left\langle #1 \right\rangle}$ $\def\om{\omega}\newcommand{\reff}[1]{(\ref{#1})}$ $\def\er{{\rm e}}\def\ri{{\rm i}}\def\C{\mathbb C}$ $\newcommand{\bce}{\begin{center}}\newcommand{\ece}{\end{center}}$

pde2path - a Matlab package for continuation and bifurcation
in 2D elliptic systems


Home | Demos | Download | Applications
Basics | First steps | Tipps/FAQ/Misc | Contact

Webpages of the old version pde2path 1.0, outdated! We strongly recommend to switch to pde2path 2.*

A first look. Our main introductory example (see First steps) is \begin{equation} {\rm Bratu's\ problem:}\label{bratu} \bf -\Delta u-f(u,\lam)=0, \quad f(u,\lam)=-10(u-\lam \exp(u)), \end{equation} $u=u(x)\in\R$, on the unit square with Neumann boundary conditions, i.e., $x\in \Om=(-1/2,1/2)^2,\ \pa_n u|_{\pa\Om}=0$. This can be set up in a few lines in pde2path to produce output as follows

(a) A first bifurcation diagram for \eqref{bratu}, (b),(c) some solution plots before and after mesh-refinement, and (d) a different plot style.

Have a preview of files for Bratu's problem? all, or separately: bratuf.m bratujac.m bratuinit.m bratucmds.m
Go to Demos for more complicated systems.