Basic usage of pde2path

This is a much shortened version of §3 of the printed manual, with links to the Matlab code (opens in new frame).
Recall that we consider

(1)

−∇⋅(c⊗∇u)+au−b⊗∇u−f = 0, with u = u(x) ∈ ℝ^N, λ ∈ ℝ, c ∈ ℝ^N×N×2×2, b ∈ ℝ^N×N×2, a ∈ ℝ^N×N and f ∈ ℝ^N,

with boundary conditions given as

(2)

n ⋅ (c ⊗∇u) + qu = g, where n is the outer normal, and q ∈ ℝ^N×N, g ∈ ℝ^N.

To explain the basic usage of pde2path we use a scalar equation, namely Bratu’s problem

(3)

−Δu + 10(u − λe^u) = 0, u = u(x) ∈ ℝ

on the unit square with Neumann boundary conditions, i.e., x ∈ Ω = (−1∕2,1∕2)², ∂_nu|_∂Ω = 0.

(3) fits into the frame (1),(2) with, e.g., c = 1, a = 0, f = −10(u − λe^u) and b = 0, and q = g = 0.

Contents

3.1.1 Installation and preparation

The basic pde2path installation consists of a root directory, called pde2path, with a subdirectory p2plib containing the actual software, a subdirectory demos with a number of subdirectory for different problems, a subdirectory octcomp, providing some basic octave compatibility, and one Matlab file setpde2path.m, which is a utility function to set the Matlab path. Each of the demos comes with a file *cmds.m, which contains the bare commands to run the example (and some comments), and with a file *demo.m, which produces more verbose output. To start we recommend to run setpde2path (without arguments) in the root directory pde2path and then change into one of the demo–directories, e.g., type cd demos/bratu in matlab. Then inspect the file bratucmds.m and copy paste the commands to the Matlab command line, or just execute bratucmds or bratudemo.

3.1.2 General structure, initialization, and continuation runs

In pde2path, a continuation and bifurcation problem is described by a structure, henceforth called p, which contains

• function handles which describe the functions c, a, b, f and the boundary conditions (and possibly some Jacobians);
• fields which describe the geometry of the problem, including the FEM mesh;
• fields which hold the current solution, i.e., u,λ and the tangent τ;
• a number of variables, switches and further functions (i.e., function handles) used to control behaviour of the continuation and bifurcation algorithm, and filenames for file output.

Studying a continuation and bifurcation problem using pde2path thus consist of:

• Setting up a files defining the coefficient functions c, a, b and f (and usually a function for the Jacobians) in (1), e.g. bratuf.m (and bratujac.m). (Here we assume that the b.c. function p.bcf is defined inline as in bratuinit.m and many of the further examples)
• Setting up an initialization function file, e.g., bratuinit filling p. The main steps are (1) define p.f and p.jac, (2) define geometry and mesh, and usually the b.c. by an inline function, (3) set the parameters and provide a starting point.
• Calling a number of pde2path functions. The basic call is p=cont(p) (a continuation run), which can be followed, e.g., by a repeated call to extend the branch.

See bratu files for the definition of functions and a typical init–routine, and stanparam.m for a description of the standard settings of switches and parameters.

The fundamental user provided functions thus are the coefficient function p.f and the additionally recommended jacobian function p.jac. To study a new problem, we thus recommend to edit copies of *init.m, the *f.m and *jac.m files of a suitable example (e.g. *=bratu for a scalar problem) in an empty directory and start with calling p=[];p=newinit(p); p=cont(p).

3.1.3 The PDE–coefficients and Jacobians

The coefficient function p.f is fundamental, and the jacobian function p.jac is recommended. The input argument u of both is the vector of nodal values, with u₁(⋅) =u(1:p.np), u₂(⋅) =u(p.np+1:2*p.np), …, u_N(⋅) =u((p.neq-1)*p.np+1:p.neq*p.np). For the outputs c,a,f,b of p.f we allow two forms, i.e., (arrays of) constants, or (arrays of) values on the triangle midpoints of the FEM–mesh, essentially as explained in the pdetoolbox documentation. There are two major ways to generate c,a,f,b from u. We first focus on f:

• Interpolate u to the triangle values (again called u), then write, e.g., f(u) in a standard Matlab way, i.e., f=-10*(u-lam*exp(u));
• Express, e.g., f as “Matlab text expression in x,y,u,ux,uy” (from the pdetoolbox documentation) with obvious meaning. For this, a parameter lam must be converted to a string. Afterwards, pdetxpd is called to evaluate the text expression on the triangle midpoints.

Typically we use the first syntax, bratuf, but for (3) we also provide bratuft.m as a template.

For c, which in principle is the tensor c_11kl = 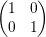we simply write c=1 which corresponds to the simplest symmetric case, and we use a = 0. There are various special coding schemes for diagonal or symmetric c and a, see the pdetoolbox documentation.

The tensor b = b_ijk, i,j = 1,…,N, k = 1,2 in (1) is not part of the pdetoolbox, but has been implemented in assemadv. Its coding and storage mimics that of c. In detail, b is an 2N² × m array where m = 1 (constant case) or m =p.nt in the order

(4)

b = b₁₁₁;b₁₁₂;b₂₁₁;b₂₁₂;…b_N11;b_N12; b₁₂₁;b₁₂₂;…;b_N21;b_N22; … b_1N1;…;b_NN2

i.e., b_ijk is in row 2N(j − 1) + 2i + k − 2.

If p.jsw< 3 then the user must also set p.jac to a function handle, here bratujac (or bratujact).

3.1.4 The geometry and the boundary conditions

The domain Ω is typically described as a polygon. For rectangles we provide a number of easy interface routines such as rec. More complicated domains can be generated via polygong.

For scalar equations the most common boundary conditions (BC) are homogeneous Dirichlet or Neumann BC. For simple cases we provide a number of interface routines such as recnbc1 for Neumann BC over rectangles. For the general case we provide the interface routines gnbc and gnbcs.

3.1.5 Error estimates and mesh adaption

pde2path comes with a posteriori error estimation and adaptive mesh refinement based on the resprective pdetoolbox routines, for instance meshref. For details see the printed manual, and for a first example see bratucmds.

3.1.6 The linear system solvers

By default pde2path uses the Matlab \ operator to solve the linear systems that appear in the Newton loops and the tangent computations. However, we never call \ directly but use two interface routines:

1.

v=p.lss(M,r,p,lam) to solve Mv = r with M = G_u ∈ ℝ^p×p;

2.

z=p.blss(A,b,p,lam) to solve Az = b with A ∈ ℝ^p+1×p+1.

Here blss and lss stand for (bordered)linear system solver, and these should be adapted for special situations.

3.1.7 Screen output, plotting, convergence failure

The screen output during runs is controlled by the two functions p.headfu (headline) and the function p.ufu. These are preset in stanparam as p.headfu=@ stanheadfu an p.ufu=@ stanufu to print a headline and, after each step, some basic information. To print some other information the user should adapt stanheadfu and stanufu to a local copy myhead.m (or similar) and set p.headfu=@myhead, and similar for p.ufu. The bifurcation diagram and solution plots are also generated during continuation runs, but in general it is more convenient to postprocess via, e.g., plotbra and plotsolf.

The files p*.mat and bp*.mat contain the complete data of the respective point on a branch. Therefore, a point can simply be reloaded by, e.g., q=loadp(pre,pname,’q’), where pre, pname is the name data of a previously saved point, and the third argument is used to set the directory name for the newly created struct. The loaded point will often be either the last one or the first; in the latter case, to change direction of the branch, use, e.g., q=loadp(’p’,’p1’,’q’); q.ds=-q.ds; q=cont(q);

If the Newton–loop does not converge even after reducing ds to dsmin then cfail is called. The standard option is to simply abort cont, but we offer a number of alternatives, e.g., to change some parameters like dsmin or imax, or to try, e.g., some mesh refinement or adaption. Clearly, the choice here is strongly problem dependent, and thus we recommend to adapt cfail.m if needed.