pict

Webpages of the old version pde2path 1.0, outdated!
We strongly recommend to switch to pde2path 2.0
________________________________________________________________________

Some background

Here we briefly explain the ideas behind some main functions of pde2path, with links to the code; for more details see the printed manual.

pde2path uses (pseudo) arclength continuation to numerically find solution branches of G(u,λ) = 0, where now G : X × ℝ → X, X = ℝⁿ, is the FEM discretization of the PDE.

Consider a branch z(s) := (u(s),λ(s)) ∈ X × ℝ parametrized by s ∈ ℝ and the extended system

( G (u, λ))
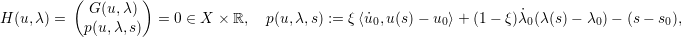H (u,λ) = p(u,λ,s) = 0 ∈ X × ℝ, p(u,λ,s) := ξ ⟨˙u0,u(s)− u0⟩+ (1 − ξ)˙λ0(λ(s)− λ0)− (s − s0),

(1)

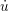where τ₀ := (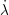

₀,

₀) :=

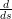(u(s),λ(s))|_s=s₀ is the tangent vector to the branch. Here 0 < ξ < 1 is a weight, and τ₀ is assumed to be normalized in the weighted norm

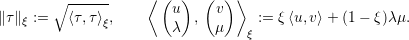
∘ ------ ⟨ ( ) ( ) ⟩ ∥τ∥ξ := ⟨τ,τ⟩ξ, u , v := ξ⟨u,v⟩+ (1 − ξ)λμ. λ μ ξ

We may then use a predictor (u¹,λ¹) = (u₀,λ₀) + dsτ₀ for a solution (1) on that hyperplane, followed by a corrector using Newtons method in the form

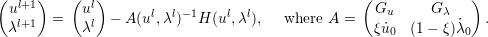( l+1 ) ( l) ( )
u = u − A(ul,λl)− 1H(ul,λl), where A = Gu G λ .
λl+1 λl ξ˙u0 (1 − ξ)˙λ0

(2)

Since ∂_sp = −1, on a smooth solution arc we have

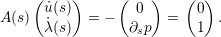(u˙(s)) ( 0 ) (0)
A (s) λ˙(s) = − ∂ p = 1 .
s

(3)

Thus, after convergence of (2) yields a new point (u₁,λ₁) with Jacobian A¹, the tangent direction τ₁ at (u₁,λ₁) with conserved orientation, i.e., ⟨τ0,τ1⟩

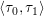= 1, can be computed from

( )
1 0
A τ1 = 1 , with normalization ∥τ1∥ξ = 1.

(4)

The main role of ξ is to balance u and λ in the continuation. Given a weight ξ, a starting point (u₀,λ₀,τ₀), and an intended step size ds, the basic continuation algorithm thus reads as follows, already including some elementary stepsize control:

Algorithm cont

1.: Predictor. Set (u¹,λ¹) = (u₀,λ₀) + dsτ₀.
2.: Newton–corrector. Iterate (2) until convergence; decrease ds if (2) fails to converge and return to 1; increase ds for the next step if (2) converges quickly;
3.: New tangent. Calculate τ₁ from (4), set (u₀,λ₀,τ₀) = (u₁,λ₁,τ₁) and return to step 1.

Theoretically, continuation does not work at possible “bifurcation points” where A is singular. More specifically, we define:

B1. A simple bifurcation point is a point (u,λ) where detA changes sign. The implicit assumption is that this happens due to a simple eigenvalue of A crossing zero.

For algorithmic reasons, for the detection of bifurcation points we only use the first part of B1, i.e., the sign change of detA, which also occurs for an odd number of eigenvalues (counting multiplicities) crossing zero. To calculate sign(det A) we only calculate the set Σ₀ of eigenvalues μ_i, i = 1,…,n_eig of A closest to 0 and then use sign( det A)=sign(Π_i=1^n_eigReμ_i). Here the implicit assumption is that n_eig is sufficiently large such that all eigenvalues with negative real part are always contained in Σ₀. This is reasonable as G_u + γ is a positive elliptic operator for sufficiently large γ.

After detection of a bifurcation between s_k and s_k+1, the bifurcation is located by a bisection method, bifdetec.

Once a bifurcation point has been saved to file, branch–switching can be performed by calling swibra.

Theory guarantees that the standard continuation algorithm converges to a given branch for “suffienctly small” ds, but near bifurcation points only in cones around the branch. Thus, near a bifurcation point it is often not useful to choose very small ds. To circumvent this and similar problems we provide the function pmcont (parallel multi continuation). Instead of using just one predictor (u¹,λ¹) = (u₀,λ₀) + p.dsτ, pmcont creates in every continuation step the predictors

(ui,λi) = (u0,λ0)+ i p.ds τ, i = 1,...,p.mst,

and starts a Newton loop for each. pmcont then monitors the convergence behaviour of each loop to decide whether it yields a “good” point, i.e., a point on the present branch.